上一讲我们学习了同态加密,这一讲我们来继续学习联邦学习中几个重要的基础概念。
不经意传输 Oblivious Transfer
不经意传输对于大部人来说比较陌生,因为它是一个密码学协议。我们首先需要了解,啥是协议。简单来说协议 protocal 是指两个或两个以上的参与者为了完成某项特定任务而采取的一系列步骤。
那么这个协议是做什么的呢?广义来说就是消息发送者从一些待发送的消息中发送某一条给接收者,但并不知道接收者具体收到了哪一条消息。不过这个协议过于宽泛,目前更加实用的版本叫做 1-2 不经意传输,在这个协议中,消息发送方每次发送 2 条消息,消息接收方只能得到其中一条,并且发送方并不知道接收方收到了哪一条。
看到这里可能大家还是一头雾水,这个协议有啥应用场景吗?你别说,还真的有,我们来看下面两个场景:
- 场景一(不经意传输):子妍和我打牌,我总是输,为了让我的游戏体验好一点,我可以看她的某一张手牌的大小,但是我并不想让她知道我看了哪张,不然很可能还是打不赢!这个场景下,就可以通过广义的不经意传输来传递牌的大小,这样可以保证我只能看到一张的大小,且子妍不知道我看了哪一张牌。
- 场景二(1-2 不经意传输):某一天我在上班路上碰到一个来自 2022 的穿越者,说 10 块卖给我两注明天就要开奖的双色球头等奖号码,但是我觉得他可能是骗子,只愿意用 5 块钱买一注试一下,而且也不愿意让他知道我选了哪一注。这个场景下,就可以通过 1-2 不经意传输来传递两注彩票,可以保证我只能拿到其中一注,并且这个穿越者不知道我能看到哪一注的号码。
接下来我们就以 1-2 不经意传输为例,介绍一下具体的协议流程(基于 RSA)。设定为发送者 Alice 的秘密是 m0,m1,Bob 想要获取到的秘密是 mb:
- Alice 产生两对 RSA 公私钥,将两个公钥 pubkey0, pubkey1 都发送给 Bob
- Bob 生成一个随机数,并用 pubkey0 或 pubkey1 加密这个随机数(想要 m0 就用 pubkey0;想要 m1 就用 pubkey1),并将密文结果发给 Alice
- Alice 用 privkey0 和 privkey1 分别解密密文,得到两个结果 k0, k1。之后用 k0 与 m0 进行异或,用 k1 与 m1 进行异或,将异或之后的结果 e0, e1 发送给 Bob
- Bob 用之前生成的随机数与 e0, e1 分别做异或操作,其中一条为真实数据,另外一条是一个随机数
这里我们重点关注第三步,因为 Alice 没办法区分 k0, k1 到底哪个是 Bob 生成的随机数,所以没办法知道 Bob 到底能够获取 m0 还是 m1。而对于 Bob 来说,因为没有私钥,所以也没办法解密另外一条数据。
另外附一张 Wiki 的介绍,非常清晰了:
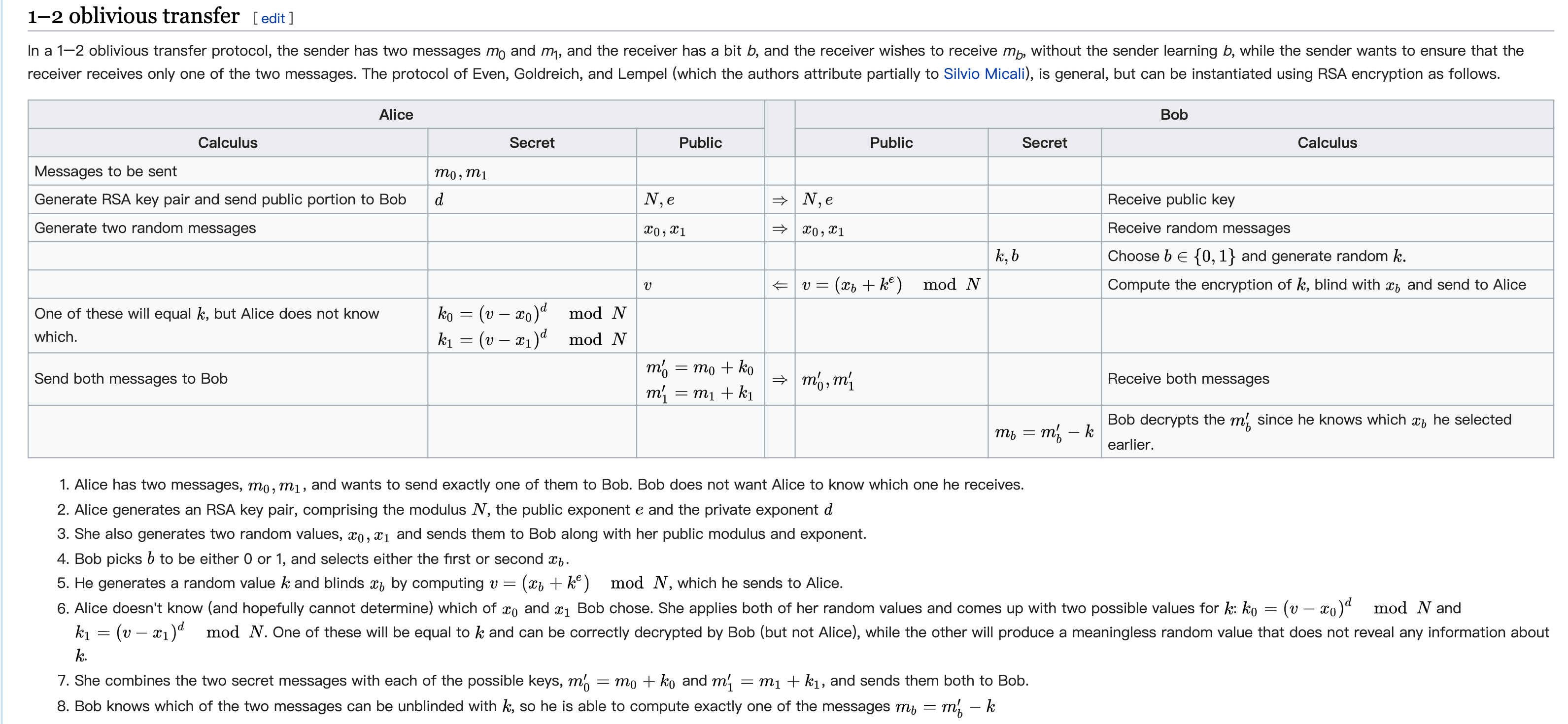
注:目前在 FATE 的实现的是 Eduard Hauck and Julian Loss 提出的不经意传输,具体参考 这里,具体在 Secure Information Retrieval 模块中使用
秘密共享 Secret Sharing
所谓秘密共享,具体的定义网上很多了,这里暂且不讲,让我先用一个具体的瞎编的场景来进行说明:
经过长达数百年的研究,人类终于掌握了时间旅行的技术,一名穿越者通过时光机来到了 1979 年,找到了一个名为 Adi Shamir 的人(就是 RSA 算法中的 S),跟他说自己正在被其他穿越者追杀,只因为手里的一份绝密情报。这份情报是黑暗森林理论,需要尽快送到红岸基地(参考三体)。穿越者本想找一个可靠的人来送情报,但担心他被干掉导致情报丢失。又想到将情报拆成七份,派七个人去送,但是万一其中一人被抓,依然没办法还原出全部的情报。所以来找 Shamir,让他帮忙出个主意。
Shamir 灵机一动,想到了一个办法,叫做门限秘密共享方案(threshold secret sharing scheme),简称门限方案。这个方案首先需要确定两个数字 n 和 m,其中 n 表示参与秘密信息共享的人数,m 表示至少几个人聚到一起才能恢复出秘密信息。那么问题来了,这个方案至少需要包括几个函数,满足几个条件?
答:需要两个函数,满足一个条件,具体如下
- 函数一:秘密分割函数,用来把秘密信息切分成 n 份
- 函数二:秘密重构函数,用来将 m 个人持有的部分秘密信息组合成完整的秘密信息
- 条件:少于 m 个人,无法正确还原
秘密分割算法
我们先回顾一下两个关键参数 n 和 m,n 是秘密信息要切分为多少份,m 是最少的恢复秘密信息的份数(设秘密信息为 s)。接下来我们需要选择一个随机的质数 $p$,同时构造一个随机的 m-1 次多项式:
$$f(x)=a_{m-1}x^{m-1}+...+a_2x^2+a_1x+a_0\ \ mod\ p$$首先,我们把秘密信息 $a_0$ 设为秘密信息 s,即 $f(0)=a_0=s$,其他的 $a$ 可以随机生成。
接着,需要选择 n 个不相同的整数,满足 $1 \le x_1,x_2,...,x_n \le p-1$,每个人获得 $k_i=f(x_i)$,需要保密自己的 $k_i$(但 $x_i$ 不需要保密,谁知道都行)
最后需要销毁 $f(x)$,就完成了秘密分割!
秘密重构算法
现在安排好的 n 个传递员每个人都有自己的 $k_i,x_i$,现在的问题就是,凑齐 m 个$k_i$ 之后,要怎么样才能还原 $f(x)$,并计算出秘密信息 $s=f(0)=a_0$ 呢?
很简单,可以通过下面的方式来重新构造出 $f(x)$
$$f(x)=\sum_{i=1}^m \frac{k_i(x-x_1)...(x-x_{i-1})(x-x_{i+1})...(x-x_m)}{(x_i-x_1)...(x_i-x_{i-1})(x_i-x_{i+1})...(x_i-x_m)}\ mod\ p$$接着我们来计算 $f(0)$ 就可以得到秘密信息 $s$
那么问题来了,为什么可以通过上面的公式来重构 $f(x)$ 呢,这里用到的就是拉格朗日插值多项式的特点,我们可以把 $(x_i,k_i)$ 看作 $f(x)$ 上的一个点,而 $f(x)$ 是 m-1 次多项式,是可通过 m 个点来唯一重构 $f(x)$ 的,并且少于 m 个点就无法重构,这也正好满足了前面提到的必备条件!
注:目前在 FATE 中实现的是 SPDZ 版本,主要用于多方安全地共同进行计算任意函数或一类函数的结果(如梯度等信息),参考 文档, 论文 1, 论文 2,
密钥交换
密钥交换是信息安全中最最基础的步骤,也是最需要保证安全的步骤,毕竟一旦密钥泄露,所谓的加密就没有任何意义了。在公开的网络里想要安全地传输信息并不简单,我们同样用一个虚构的场景,来说明密钥交换的难点。
前面提到的穿越者利用秘密共享的方式将秘密信息成功传达给红岸基地后,又面临了新的问题:他的加密时空对讲机坏了。好在他是一个 DIY 达人,用一个地球上的对讲机加上一些加密时空对讲机的零件,临时组装了一个简易时空对讲机。重新和未来的组织取得联系后,通讯员告诉他现在他们的通讯并不安全,因为其他拥有时空信号站接入权限的人都可以看到他们的通讯内容。通讯员要求穿越者之后的消息要加密后才能发送,并且需要事前约定好相同的密钥以便加密解密。问题来了,怎么发送这个密钥成了大问题,因为如果直接发送的话,其他人也能看到这个密钥!
有没有办法在这样的条件下,在不泄露密钥的前提下完成密钥的交换呢?穿越者表示“我太难了”,于是通讯员让穿越者回到 1976 年,去找 Whitfield Diffie 和 Martin Hellman 帮忙。
顺利找到 Diffie 和 Hellman 之后,他们对穿越者表示你这个问题我们刚好能解决,哪怕有窃听者也没问题,按照下面的步骤来就可以:
- 穿越者需要先找一个很大的质数 $p$,以及 $p$ 的一个原根 $g$(后面会具体说明这个概念),然后通过对讲机告诉通讯员。与此同时,窃听者也能知道 $p$ 和 $g$,但不用紧张,这俩是公钥,大家都知道也没问题。
- 穿越者随机选择一个数字 $r_1$,通讯员也随机选择一个数字 $r_2$。注意,这两个数值就是私钥,千万不能通过对讲机提起,不然窃听者知道了就全完了。
- 穿越者计算 $ret_1=g^{r_1}\ mod\ p$ 并发送给通讯员;通讯员计算 $ret_2=g^{r_2}\ mod\ p$ 并发送给穿越者。这两个计算结果窃听者也可以知道,但不怕,他还原不了 $r_1, r_2$(后面会具体说明)
- 穿越者计算 $ret_2^{r_1}\ mod\ p = g^{r_1r_2}\ mod\ p$,通讯员计算 $ret_1^{r_2}\ mod\ p = g^{r_2r_1}\ mod\ p$
- 现在穿越者和通讯员都知道一个相同的密钥 $g^{r_1r_2}\ mod\ p$,并且窃听者完全没办法猜出来,这样就完成了密钥交换,接下来就可以用这个密钥进行通讯了。
那么这个算法是如何保证安全的呢?网上的很多材料都会有这么一句:因为在有限域上计算离散对数非常困难。问题来了,啥是离散对数,为啥非常困难呢?还有前面提到的原根,到底是什么?
我们先来讲一下啥是原根。对于一个质数 $p$,如果有一个数字 $a$,使得 $a\ mod\ p,\ a^2\ mod\ p,…,a^{p-1}\ mod\ p$ 的数值各不相同,且包括了从 $1$ 到 $p-1$ 的所有整数,那么 $a$ 就是 $p$ 的一个原根。
接下来就可以来看看啥是离散对数了。如果对于一个整数 $b$、一个质数 $p$ 和它的原根 $a$,可以找到一个唯一的指数 $i$,使得 $b=a^i\ mod\ p,\ 0 \le i\le p-1$,那么指数 $i$ 被称为 $b$ 的以 $a$ 为基数的模 $p$ 的离散对数。
离散对数有一个特点:已知 $p$ 和 $a$ 之后,对于给定的 $b$ 要计算 $i$ 很难,但是对于给定的 $i$ 计算 $b$ 是很容易的。之所有有这种特性,是因为取模这个操作是一个单向函数(one-way function),即计算起来容易,但求逆很难。这个特性也就使得大部分公开密钥密码协议,都离不开取模这个操作(如前面介绍过的 Paillier 和 RSA)
注:DH 密钥交换算法易受到中间人攻击,可以通过数字签名进行保护,这里不展开说明,感兴趣的同学可以查看下面的参考链接。在 FATE 中主要用做多方数据表操作的底层安全保护。
差分隐私 Differential Privacy
前面介绍的各种方法,最终的目标都是为了保护数据隐私,基本都属于密码学方法,即通过不将输入值传给其他参与方的方式或者不以明文方式传输,使分布式计算过程安全化。另一种常见的方法是模糊处理(Obfuscation),指的是随机化、添加噪声或修改数据使其拥有某一级别的隐私,如差分隐私。
差分隐私这个词被大众熟知是在 2016 年苹果的 WWDC 大会:用户数据加密后上传到苹果服务器后,苹果可以用这些加密后的数据计算出用户群体的相关特征,但无法解析某个个体的信息。不过差分隐私并非苹果原创,来自微软的 C. Dwork 早在 2006 年便首次提出差分隐私的概念。
举一个贴近生活的例子,假如我们班 50 个同学举办毕业晚会,最后有抽奖环节,特等奖一共 5 名,为了保持神秘,并不公布名单。所谓差分攻击,就是当我打听到了其他 48 个同学的中奖情况,实际上第 49 个同学是否中特等奖我也就知道了(如果包括我在内的 49 个同学已有 5 人特等奖,那么最后一个同学肯定没中奖;如果只有 4 人中奖,那么最后一个同学就肯定中奖了)。
差分隐私正是为了应对差分攻击而生,简单来说就是给查询结果加噪声(实际上,也可以对源数据/模型参数加噪声),但是一定要恰到好处。噪声加太大,数据集得出的统计值就没有意义了;而噪声加太小,还是很容易被差分攻击攻破,无法保证隐私。用上面特等奖的例子来说,就是在打听除自己外 48 个同学的信息时,让有些人不说实话,那么我就无法推断第 49 名同学是否真正中奖了。
注:本节来源于我在微众时写的科普文章 联邦广告:技术捍卫隐私,节选用做简单的差分隐私介绍